目次
記述統計
統計の手法には記述統計と推測統計があると説明したが、ここでは記述統計の話。記述統計の考え方を通じて、より進んだデータの見方を学んでいく。
記述統計とは
記述統計とはすべてのデータを見て正しく全容を把握・認識するための方法論・作法。
全てのデータを見るのでデータマイニング的なアプローチ。
仮説ありきではないので、記述統計の方法だけではデータの組み合わせが膨大だと有効な知見を得るに至らないこともある。
後でどんな手法を使う際にも、それは推測統計や機械学習の手法を使う場合であっても、データを見るという観点ですべての基本の考え方になる。
データの種類
データは特徴によって分類される。
種類によってデータ加工方法から分析手法も変わってくる。
どんな観点で分類するのか、分類のポイントを紹介していく。
尺度
尺度とは、ざっくり言うと数字のなす意味、その数字が対象の特徴をどのように説明するかによる分類。こう言うと難しいので、実際の内容を具体的に見ていこう。
- 定性的データ(カテゴリカルデータ)
- 名義尺度:数字は単なる名前・ラベルであって、その大小に意味はない。
(例)性別/1=男性、2=女性 - 順序尺度:大小比較できる。ただし差に意味はない。
(例)満足度/1=不満、2=どちらでもない、3=満足
- 名義尺度:数字は単なる名前・ラベルであって、その大小に意味はない。
- 定量的データ
- 間隔尺度:差に意味がある。比に意味はない。つまり割り算する意味がない
(例)温度(℃)「30℃は15℃の2倍」とは言わない、日付 - 比例尺度、比尺度:比率にも意味がある。0が基準となるもの。
(例)身長、訪問客数
- 間隔尺度:差に意味がある。比に意味はない。つまり割り算する意味がない
下の尺度は上の尺度の性質をすべて含む。尺度によって使える分析手法が異なる。
変数の数
変数の数による分類。
- 1次元データ
- 2次元データ
- 多次元データ
ビジネスの世界で実際に直面するデータは多次元データばかりだろう。
データセットの種類
タイミングと観測対象によって分類
- 横断面(クロスセクション)データ
1つの時間を切り取って(同じタイミング)、その中で複数の対象(顧客など)についてのデータ - 時系列データ
1つの対象についての時間経過とともに記録したデータ - パネルデータ
クロスセクションかつ時系列のデータ、複数対象の時をまたいだデータ。購買履歴などの履歴データや、同じ対象に対する同一アンケート調査を毎年行ったデータ(横断面データを定期的に収集していったもの)がこれに該当する。
生ログ or 集計済みデータ
データというのは
自動取得されるアクセスログや、実査を行うアンケートであれば個票データになる大元のデータ
があり、それを
アクセス解析ツールやアンケート集計ツールを使って集計された形でアウトプットが出てくる
という流れになっていることが多い。
この大元の生のデータか、それとも集計済みのデータか、それが大きな分類となる。
- アンケート調査:個票データ or 集計データ
- アクセス解析:webサーバの生ログ or GAの管理画面のデータ
生ログは情報自体は豊富に含まれるのだが、人間が見ても分かりにくい、認識しにくいものである。
わかりやすく集計されたデータを見れば何が起こっているか、データの意味がよくわかる。
だからわれわれは集計済のデータを使って分析するのが基本である。
生ログからはいかようにも集計が可能だが、一度集計されてしまうとログに戻すことはできない。
集計は何らかの情報を切り取る作業であり、データのサイズは小さくなる(ことが多い)が、同時に失われる情報もある。
通常生ログから集計を何ステップか経てデータを扱うが、データを保持するとき、どの段階のものを保持するのか、その後の利用シナリオを考慮したうえで設計する必要がある。
集計データを扱う場合、集計の過程で
- 集計の切り口が限定されてしまい、任意の変数の関係を見ることができない
- 何らかのロジックに基づいて分類を行った場合、その分類ロジックがブラックボックスになってしまう。たとえばアンケート結果を要約してポジティブ/ネガティブと分類したうえで集計した場合、ポジティブ/ネガティブの分類基準は集計結果データには含まれない。
ことに留意する必要がある。
代表値とばらつき
データの特徴を一言で、ではなく、一つの数値で表したもの。
代表値(中心傾向)
代表値はデータを代表する、データを一言で言い表す値。たとえば身長のデータだったら「大体このくらいの長さだよね」というのが代表値を意味する。それそのものでは意味の分からない「○○指数」のようなものであったとしても、「この○○指数というのは大体このくらいの大きさだよね」というのが最初の議論になるだろう。
つまりデータの中心の位置、数値の大小を表すものになる。
- 算術平均(mean)
一般的な平均の概念。観測値の合計を個数で割る。
$$\bar{x} = \frac{1}{n} \sum^n_{i=1} x_i$$
外れ値や歪んだ分布に弱い(外れ値があると算術平均値が変わる、分布がの歪みが少し極端になるだけで算術平均値が変わる) - 中央値(median)
データを下から順に並べてちょうど真ん中の番目の観測値- データの個数が奇数(たとえば19個)の場合、10番目の値
- データの個数が偶数(たとえば20個)の場合、10番目の値と11番目の値の算術平均(真ん中がないため)
- 最頻値(mode)
データの中で最も頻出する値- 変数が離散の場合、そのまま最も頻出する観測値を指す
- 変数が連続の場合、データをいくつかの等間隔の区間に区切ってヒストグラムにしたときの、最も頻度が高い区間を指す(基本的に同じ値が発生するものではないため)
- 刈り込み平均(trimmed mean)
データの上下○%の順位のデータを除外した残りの観測値の算術平均
中央値、刈り込み平均は外れ値や歪んだ分布に対しても頑健(外れ値があっても中央値は変わらない、分布が少々歪んでも中央値は変わらない)。
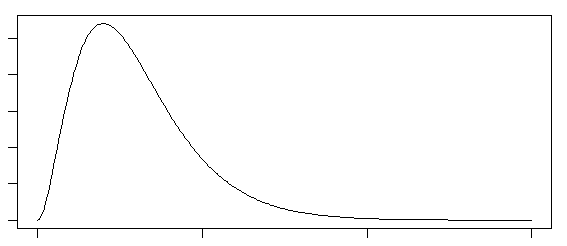
このような分布においては
最頻値<中央値<算術平均
となる。
ばらつきの指標
代表値は数値の大小を議論するものだったが、
こちらは数値がどれだけばらついているかという観点である。
- 範囲
最大値と最小値の差。
データに外れ値があるとその値が最小値や最大値になるため、外れ値に影響されやすい - 分散
$$s^2 = \frac{1}{n} \sum^n_{i=1} (x_i – \bar{x})^2$$
すべての観測値に対する算術平均との差の2乗の(算術)平均値。外れ値に影響されやすい。- 標準偏差
$$s = \sqrt{\frac{1}{n} \sum^n_{i=1} (x_i – \bar{x})^2}$$
分散はオーダーが観測値の2乗になっているため、平方根を取って観測値のオーダーに戻したもの
- 標準偏差
- 平均絶対偏差(MAD)
$$MAD = \frac{1}{n} \sum^n_{i=1} | x_i – \bar{x} |$$
分散/標準偏差では観測値と算術平均との差の2乗を取ったが、観測値と算術平均の差の絶対値をとったもの。 - 四分位範囲
25%点(第1四分位数)と75%点(第3四分位数)の差- 四分位偏差
四分位範囲を2で割ったもの
四分位範囲と四分位偏差、こちらも順位に関する統計量だが、外れ値があっても影響されない。
- 四分位偏差
同じ平均でもばらつきが大きいか小さいかで意味は変わってくる。
さらに分布が左右対称でない場合もあるが、ばらつきの指標ではそれも分からない。
単に代表値だけを比較するのではなく、分布を見るのが重要。
分析手法には特定の分布を前提としているものが多く、分布を見ないと危険である。
順位に関する統計量(中央値、四分位範囲など)は外れ値や分布の形状に大きく左右されない(頑健、ロバスト)。
分布がゆがんでもそれなりに意味をなすという意味で、結構便利。
逆に算術平均、分散などは分布がゆがむと意味をなさなくなる。
外れ値
代表値とばらつきの項目ですでに出てきたが、外れ値とは
「平均的な観測値から大きく離れた値」
算術平均や分散を使った一般的な手法の分析に大きな影響を及ぼし、分析結果を使い物にならないものにしてしまうため、
- 外れ値を除外して分析する
- 外れ値に影響されにくい分析方法を採用する
などの対応が必要になる。
また外れ値が発生する場合、その原因を念頭に置いておかないと、それが本当に意味をなさないデータなのか、意味はあるが分析結果を壊すために分析対象から除外しなければならないものなのか分からない。それによって分析結果の意味も変わってくるはずなのに。
偏り(バイアス)
同じコンバージョン率でも、
- 「性別問わず完全にランダム」
- 「男性のほうがコンバージョンしやすい」
では意味が違う。この「○○だったら△△しやすい」という傾向を偏りという。
分析の目的は「特定の傾向」を導くことでもあるので、平均値や分散が同じであったとしても、特定の傾向があるかどうかで結果の意味が変わってくる。
ばらつきというのはランダムなもののことを指し、ランダムでない傾向を偏りという。
多くの統計手法でランダムなばらつきか偏りなのかによって扱い方が変わってくるので、この見極めが重要となる。
ばらつきの考え方
- もともとばらつきの大きいデータなら、少し離れた値でも正常値(偶然の範囲)。
- もともとばらつきの小さいデータなら、少し離れただけで問題に。
数学の得点の「性別間のばらつき」が「同じ性別内のばらつき」に比べて大きければ、性別の違いに意味がある
※全体のばらつき=グループ間のばらつき+グループ内のばらつき
単純平均と加重平均
「バナーAがCTR=0.07%、バナーBのCTR=0.13%のとき、キャンペーン全体のCTRは?」
実は
- バナーAのインプレッション数=50,000
- バナーBのインプレッション数=10,000
-
(0.07+0.13)÷2=0.1%
→単純平均 - (0.07×50,000+0.13×10,000)÷60,000=0.08%
→加重平均
単純平均が適切な場合と加重平均が適切な場合がある
シンプソンのパラドックス
2つの高校の英語のテストの平均点を比較
| 男子 | 女子 | |
|---|---|---|
| 高校A | 80点 | 60点 |
| 高校B | 90点 | 70点 |
どちらの学校が優秀?
まあこれだけ見ると高校Bのほうが男女いずれも平均点が高く優秀ということになる見えるが、もしこういう事情があったらどうなるか。
| 男子 | 女子 | |
|---|---|---|
| 高校A | 90人 | 10人 |
| 高校B | 10人 | 90人 |
トータルの平均点にすると、
| 高校A | 78点 |
| 高校B | 72点 |
高校Aの平均点のほうが高くなる。
ということで、分割の仕方(ここでは男女の人数)によっては結論が逆になるというのがシンプソンのパラドックスである。
相関、因果、独立
相関関係
AとBの間の関係。Aが増えるとBも増える?減る?
厳密には相関係数はAとBの間の線形の関係、つまり1次関数で表される関係である。両者の関係が線形でない場合に相関係数は意味をなさない。
因果関係
データそのものから因果関係はわからない。「AだからB」を成立させる理論があって、かつデータがそれを示している場合のみ因果関係があるといえる。
データ上は関係が見られたものの、中には「偶然の一致」のケースもある。
因果関係があれば相関関係は発生する。相関関係があるからといって因果関係があるとは限らない。
「AとBの間に相関がある」といっても「AだからB」なのか、「BだからA」なのか、それとも偶然の一致なのか、
データとは別に理論がないと判断がつかないのである。
たとえば「広告投下量」と「認知度」の間には相関がある。しかし認知度が高いから広告投下量が多くなるわけではない。広告投下量が多いから認知度が高くなる。下支えするロジックがないと因果関係があると言えないのである。
交絡因子
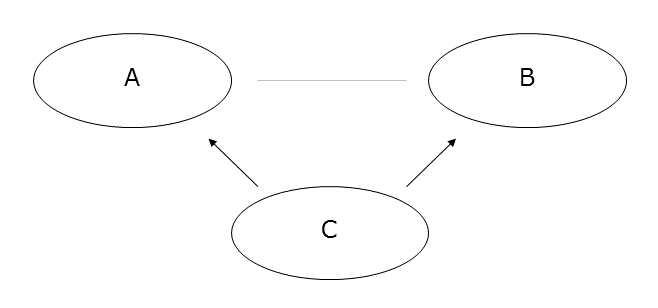
交絡因子とは、現在見ている変数に対して、共通に影響を及ぼしている変数を指す。
上の図ではCがAとBに対して共通して影響を及ぼす交絡因子となっており、この場合AとBの間に相関関係が発生する。
交絡因子がある場合も相関は発生する。しかしそれは実質的な意味はない、見かけ上の相関である。これを疑似相関という。
たとえば、アイスクリームの売上が伸びると、水死者数も確実に増える。だからといってアイスクリームの売上と水死者数に因果関係はない。夏だからという季節、気温が両現象の共通した背景にある。
複数の現象の背後に共通して潜む因子がある場合、それが交絡因子となる。
独立
$$P(A) = P(A|B)$$
Aが発生する確率はBの生起とは無関係
統計の世界ではよく出てくる「独立」という言葉の正確な意味がこれである。
可視化
上でデータの代表値やばらつきの指標を見るだけではなく分布を見ることが重要だと説明した。
ということで、分布を見るためにチャートを作ってデータを図示する定石を説明する。
必要なチャート
- 散布図(点でプロット→位置で認識)
- 棒グラフ(定性データ、長さで量を認識)
- ヒストグラム(定量データ、分布)
- 折れ線グラフ(推移)
- 箱ひげ図(複数の分布を並べて比較)
データを正しく把握するためにはこれらのチャートだけで十分。
というのも人間は位置と長さでしか正確に量を認識できないからである。
これ以外のチャート、たとえば円グラフ、レーダーチャート、面積で表すもの(バブルチャートなど)では正しく数量を把握しにくい。
何かを強調して誘導するために違う種類のチャートを使うことは有効である。
散布図
複数の変数の関係を見るのによく使う
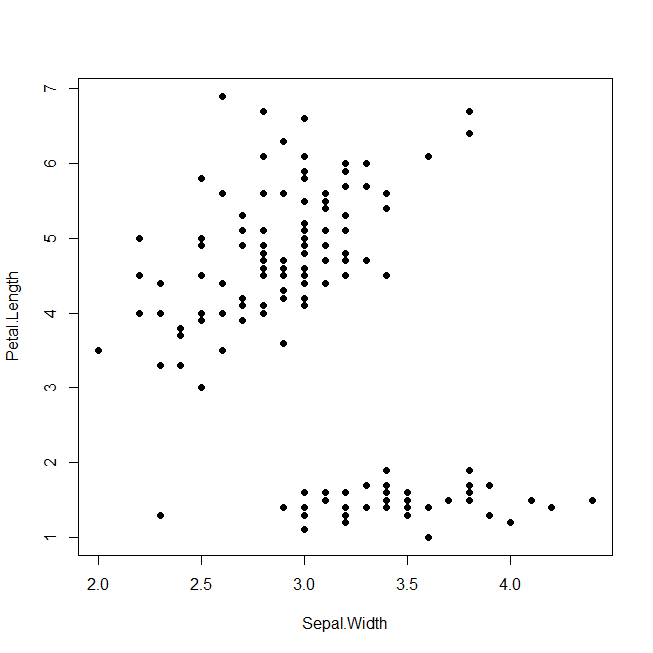
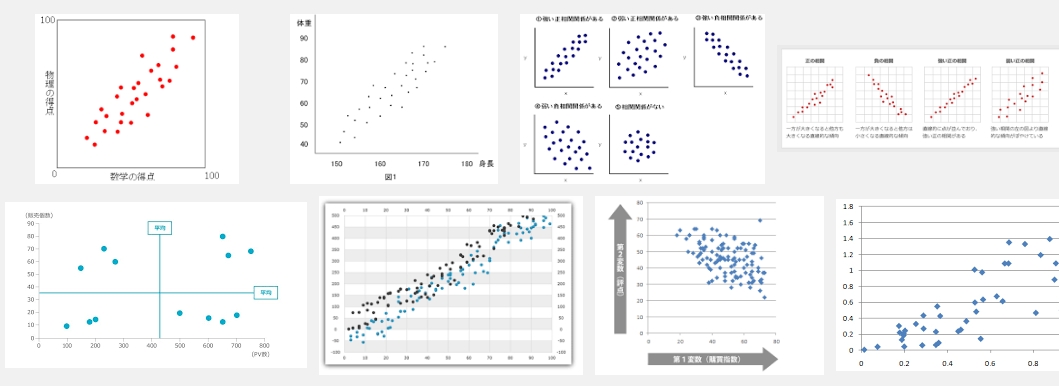
棒グラフ
グループ間の比較
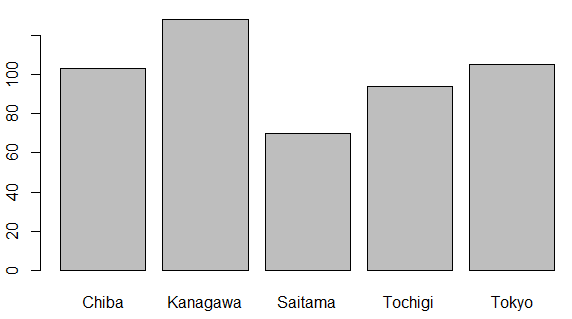
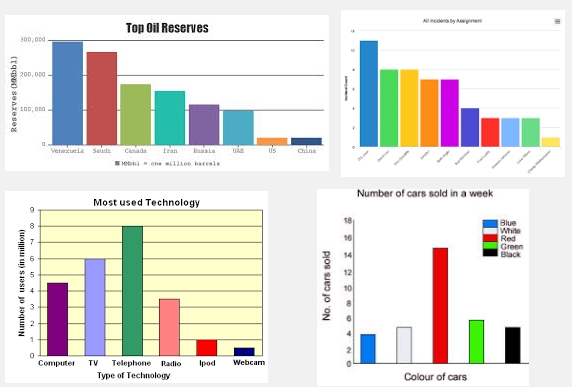
ヒストグラム
1変数の分布を見る
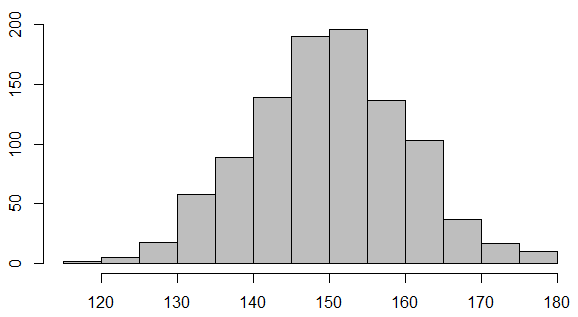
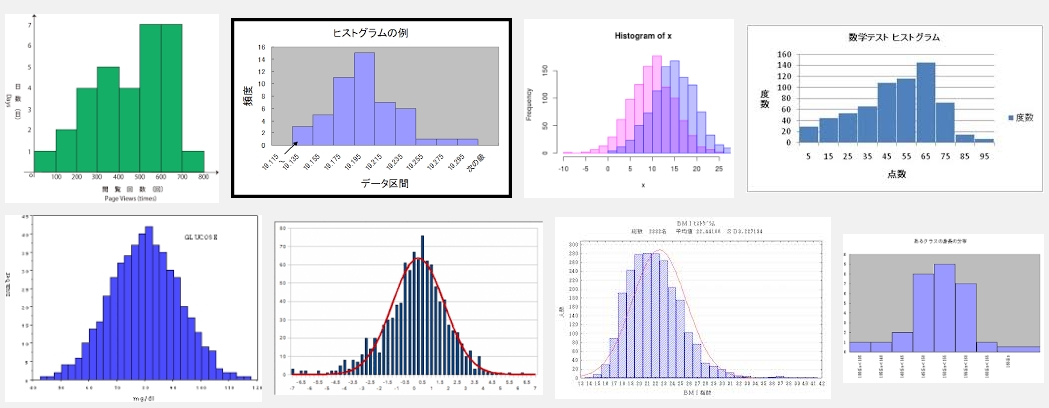
折れ線グラフ
時系列で見るときに使う
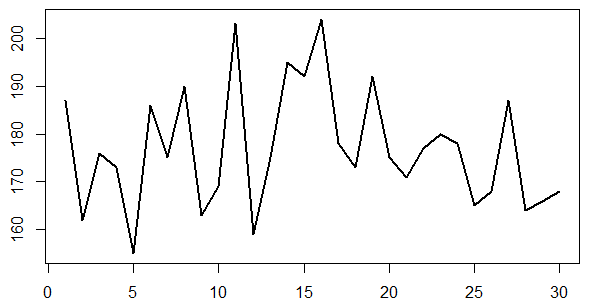
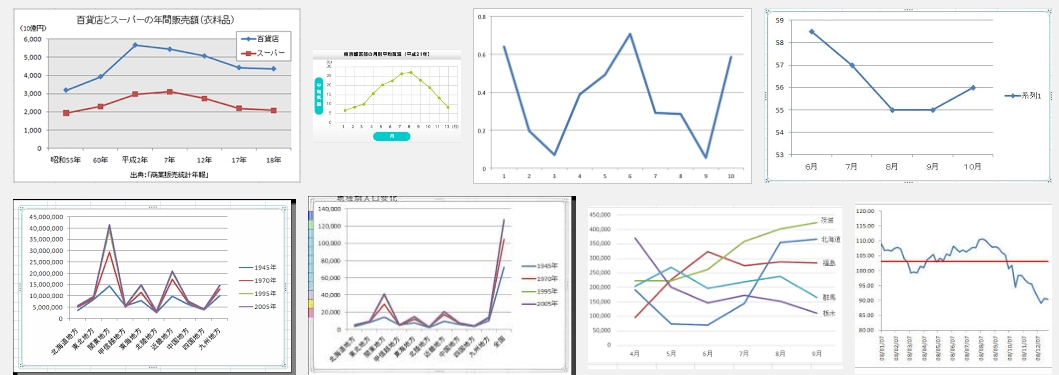
箱ひげ図
グループ間で分布を比較する
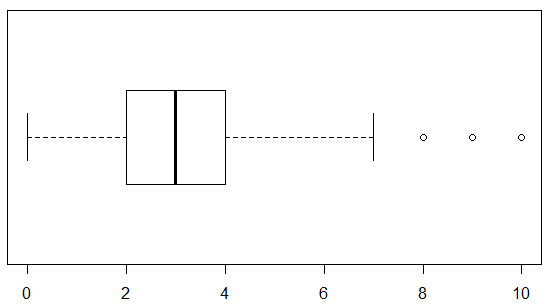
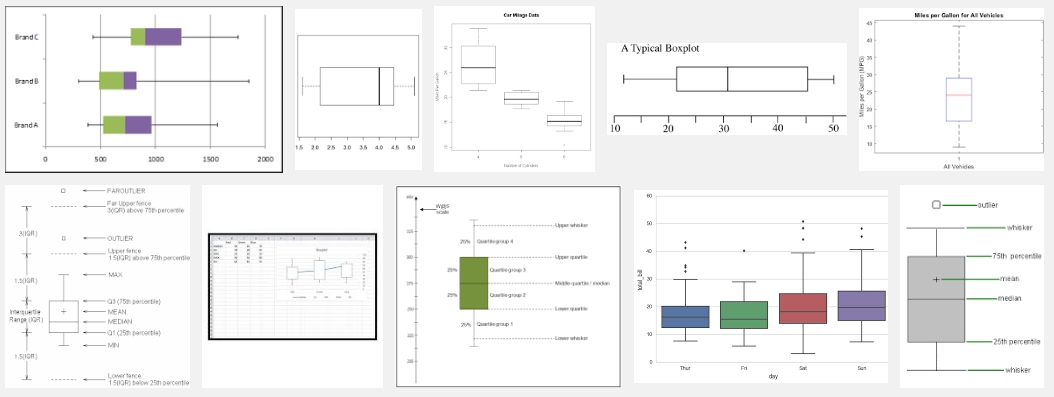
真ん中の区切られた長方形の
- 下端が第1四分位点(25%点)
- 真ん中の区切り線が中央値(50%点)
- 上端が第3四分位点(75%点)
両端の○が外れ値
長方形から上下に伸びたひげの終点にはさまざまな基準がある。
(代表的なものは各四分位点から外側に四分位範囲の1.5倍だけ離れた点)
探索的データ解析(EDA)
データを眺めることについてのより進んだ理論。
データをプロットし、分布を見る。どんな分布に当てはまるか把握する。わかりやすく可視化する。
handbook of Exploratory Data Analysis
変数のタイプに応じたアドバンストなチャートの一覧
Graphical Techniques: By Problem Category
データ分析 の記事一覧




