クラスター分析は

1. 距離行列の生成（類似度行列ではない！）
2. クラスタリングの実行

という流れになる。

それぞれのステップで、採用する

• 距離の種類
• クラスタリングの方法

がチューニング変数となる。
この順に手順を見ていく。

行数、列数の多いビッグデータ向きのデータ形式であるMatrixパッケージに対応した距離行列についても説明する。

距離行列を生成する

類似度行列ではなく距離行列を作る。similarityではなくdistanceを作る。
直感的にはデータから距離の指標（どれだけ離れているか）ではなく類似度（どれだけ近いか）の指標を抽出し、そこからクラスタリングしたいケースが多いのだが、あくまで類似度指標に基づいた距離行列を生成するのである。

通常のdist関数では対応する距離の種類が少ないのでproxyパッケージを使う。
距離行列を生成するメソッドはdist(data, method="距離の種類")。

require(proxy)
dcos <- proxy::dist(USArrests, method="cosine")

戻り値はdistオブジェクト。行列やデータフレームとは異なるので扱いに注意。
distオブジェクトは同じ次元なら加減乗除が可能。たとえばdist1, dist2ともにdistオブジェクトの場合、

dist1 + dist2
dist1 - dist2
dist1 * dist2
dist1 / dist2

いずれも対応する要素を加減乗除したdistオブジェクトとして返ってくる。

類似度の種類

類似度（どれだけ近いか）の種類と、それに対応したdist()関数で指定する引数methodの値

• 数値ベクトルに対するもの
  • コサイン類似度: cosine
  • 拡張Jaccard: eJaccard
  • fuzzy Jaccard: fJaccard
  • Pearsonの積率相関係数: correlation
• 0/1値に対するもの（集合に入る or not）
  • Jaccard係数: Jaccard
  • Simpson係数: Simpson
  • Dice係数: Dice
  • Simpson-Jaccard係数は直接算出できないが、(dSimpson + dJaccard) / 2とするだけでSimpson-Jaccardの距離行列を取得できる
• 2×2の分割表に対するもの
  • ファイ係数: Phi
  • ユールのQ: Yule

（参考）主な類似度指標の違い

数値ベクトルの類似度では、
Pearsonの積率相関係数は、各成分から平均値を引いたもののcos類似度と一致する

２値変数の類似度指標は基本的に

$$
\frac{共通部分}{2集合の【何か】}
$$

【何か】が指標によって異なる。

• Jaccard係数→和集合
• Simpson係数→共通部分
• Dice係数は→算術平均

Simpson-Jaccard指数はSimpson指数とJaccard指数の算術平均。
Diceは分母が算術平均になるという違いがある（調和平均に似ている）。

距離の種類→数値ベクトルに対するもの

距離（どれだけ離れているか）の種類と、それに対応したdist()関数で指定する引数methodの値

• ユークリッド距離: Euclidean
• マハラノビス距離: Mahalanobis
• マンハッタン距離: Manhattan
• チェビシェフ距離: Chebyshev
• ミンコフスキー距離: Minkowski
• キャンベラ距離: Canberra

たとえば

# コサイン類似度に基づく距離
dcos <- proxy::dist(USArrests, method="cosine")
# 連続量版Jaccard係数
djcd <- proxy::dist(USArrests, method="eJaccard")
# ピアソンの積率相関係数に基づく距離
dcor <- proxy::dist(USArrests, method="correlation")

などとなる。

Matrix形式の行列に対する類似度の算出関数

Rの通常の行列やデータフレームではディメンションの大きいsparse matrix（疎行列）を扱うのが困難である。
Matrixというパッケージは行列を独自の形式で扱うパッケージで、主にsparse matrixなどを扱うのに強い。
このMatrix形式の行列に対して類似度を計算する関数を作った。

• jcdSparse(): バイナリデータに対するJaccard係数
• smpSparse(): バイナリデータに対するSimpson係数
• ejcdSparse(): 連続量に拡張したJaccard係数
• esmpSparse(): 連続量に拡張したSimpson係数
• cosSparse(): コサイン類似度

jcdSparse <- function(X){
    X <- as(X, "dgCMatrix")
    X@x <- rep(1, length(X@x)) # 非ゼロ要素はすべて1に置換
    vec_sum_col <- colSums(X)
    AB <- crossprod(X)
    sim <- AB / (vec_sum_col - t(AB - vec_sum_col)) # まとめて
    return(sim)
}

smpSparse <- function(X){
    X <- as(X, "dgCMatrix")
    X@x <- rep(1, length(X@x)) # 非ゼロ要素はすべて1に置換
    vec_sum_col <- colSums(X)
    AB <- crossprod(X)
    n <- length(vec_sum_col)
    A <- matrix(rep(vec_sum_col, n), n)
    B <- t(A)
    mat_A_lt_B <- A < B
    sim <- AB / (A * mat_A_lt_B + B * (1 - mat_A_lt_B))
    return(sim)
}

ejcdSparse <- function(X){
    X <- as(X, "dgCMatrix")
    vec_xx <- colSums(X^2)
    mat_xy <- crossprod(X)
    sim <- mat_xy / (vec_xx - t(mat_xy - vec_xx)) # まとめて
    return(sim)
}

esmpSparse <- function(X){
    X <- as(X, "dgCMatrix")
    vec_xx <- colSums(X^2)
    mat_xy <- crossprod(X)
    n <- length(vec_xx)
    mat_xx <- matrix(rep(vec_xx, n), n)
    mat_yy <- t(mat_xx)
    mat_x_lt_y <- mat_xx < mat_yy
    sim <- mat_xy / (mat_xx * mat_x_lt_y + mat_yy * (1 - mat_x_lt_y))
    return(sim)
}

cosSparse <- function (X) {
    if(class(X)[[1]] != "dgCMatrix") {
        X <- as(X, "dgCMatrix")
    }
    X_normalized_col <- X %*% Diagonal(x = 1 / sqrt(colSums(X^2))) # まとめて
    sim <- crossprod(X_normalized_col)
    return(sim)
}

距離行列と類似度行列の関係

• 類似度は一致するときに1をとる。独立なら0、正反対なら-1
• 距離は大きいほうが離れている

distance = 1 - similarity

Pearsonの積率相関係数から距離行列を生成するのもこの原理。

（参考）

• 類似度と距離の概念
  http://wikiwiki.jp/cattail/?%CE%E0%BB%F7%C5%D9%A4%C8%B5%F7%CE%A5
• その他の距離
  http://www.nysol.sakura.ne.jp/mcmd/jp/sect-msim.html
• 直接実装するなら
  http://sucrose.hatenablog.com/entry/2012/11/30/132803
• 距離に関するRのライブラリと関数
  http://www.slideshare.net/yuifu/ss-11776646
• {proxy}パッケージに実装されている距離と類似度の一覧
  https://cran.r-project.org/web/packages/proxy/vignettes/overview.pdf

主成分分析とクラスタリング

主成分分析のprcomp()関数についておさらい

• prcomp$xが主成分得点行列
• prcomp$sdevが固有値
• prcomp$rotationが固有ベクトル
• biplot(prcomp)でプロット
• 主成分得点×固有ベクトル＝相関行列（scale=Tで実行した場合）
• prcomp()とprincomp()関数の違い：
  • prcomp()関数：主成分得点を求める際に、主成分得点の不偏分散が固有値に一致するように計算される
  • princomp()関数：主成分得点の標本分散が固有値に一致するように計算される

主成分分析を行い、第1主成分と第2主成分をクラスタリング

# 主成分分析
USArrests.prcomp <- prcomp(USArrests, scale = TRUE)
## 第１主成分から第2主成分の主成分得点を抽出
USArrests.scores <- USArrests.prcomp$x[,1:2]

クラスタリング

# 3個のクラスタに分類
USArrests.kmeans <- kmeans(USArrests.scores, centers = 3)
# クラスタサイズ確認
table(USArrests.kmeans$cluster)

プロット

# 第１主成分得点
USArrests.pc1 <- USArrests.prcomp$x[,1]
# 第2主成分得点
USArrests.pc2 <- USArrests.prcomp$x[,2]
# クラスタ
USArrests.clusters <- USArrests.kmeans$cluster

# plot関数でプロットする場合
plot(USArrests.pc1, USArrests.pc2, xlab = "PC1", ylab = "PC2", col = USArrests.clusters)

## ggplot2でプロットする場合
USArrests.pc.df <- data.frame(
    State = rownames(USArrests), 
    PC1 = USArrests.pc1, 
    PC2 = USArrests.pc2, 
    Cluster = factor(USArrests.clusters)
)
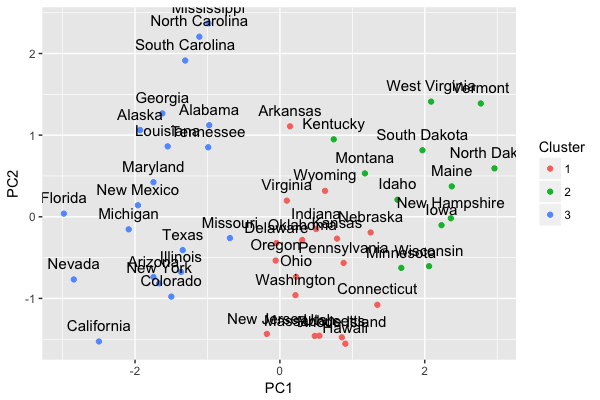
ggplot(USArrests.pc.df, aes(x = PC1, y = PC2, label = State, color = Cluster)) + 
       geom_point() + geom_text(size = 4, colour = "black", vjust = -1)

http://www.statmethods.net/advstats/cluster.html

クラスタリングの実行

階層的クラスタリング

ユーザ分類などビッグデータには不向き。
階層的クラスタリングを実行するメソッドはhclust(dist, method="クラスタリングの方法")。
引数で与えるのは距離行列

hclust()の引数methodの種類

• 最近隣法: single
• 最遠隣法: complete
• 群平均法＝UPGMA: average
• 重心法＝UPGMC: centroid
• メディアン法＝WPGMC: median
• Ward法＝最小分散法（郡内分散と群間分散の比を最大化）: ward.D2
• McQuitty法＝WPGMA: mcquitty

デンドログラムの生成

距離の種類×クラスタリングの手法で比較するよね。

• コサイン類似度の距離行列dcos
• Jaccard係数の距離行列djcd
• Simpson係数の距離行列dsmp
• Tanimoto係数の距離行列dtnm
• Dice係数の距離行列ddce

に対して

• Ward法
• 群平均法（UPGMA）
• McQuitty法

で階層クラスタリングした結果をデンドログラムで比較する。

pdf("hclust.pdf")
op <- par(mfrow=c(2,3))
{ # Ward法
    wd.dcos <- hclust(dcos, method="ward.D2")
    wd.djcd <- hclust(djcd, method="ward.D2")
    wd.dsmp <- hclust(dsmp, method="ward.D2")
    wd.dtnm <- hclust(dtnm, method="ward.D2")
    wd.ddce <- hclust(ddce, method="ward.D2")

    plot(wd.dcos, main="cosine similarity/Ward")
    plot(wd.djcd, main="Jaccard index/Ward")
    plot(wd.dsmp, main="Simpson index/Ward")
    plot(wd.dtnm, main="Tanimoto index/Ward")
    plot(wd.ddce, main="Dice index/Ward")
}
par(op)
op <- par(mfrow=c(2,3))
{ # 群平均法（UPGMA）
    ga.dcos <- hclust(dcos, method="average")
    ga.djcd <- hclust(djcd, method="average")
    ga.dsmp <- hclust(dsmp, method="average")
    ga.dtnm <- hclust(dtnm, method="average")
    ga.ddce <- hclust(ddce, method="average")

    plot(ga.dcos, main="cosine similarity/UPGMA")
    plot(ga.djcd, main="Jaccard index/UPGMA")
    plot(ga.dsmp, main="Simpson index/UPGMA")
    plot(ga.dtnm, main="Tanimoto index/UPGMA")
    plot(ga.ddce, main="Dice index/UPGMA")
}
par(op)
op <- par(mfrow=c(2,3))
{ # McQuitty法
    mq.dcos <- hclust(dcos, method="mcquitty")
    mq.djcd <- hclust(djcd, method="mcquitty")
    mq.dsmp <- hclust(dsmp, method="mcquitty")
    mq.dtnm <- hclust(dtnm, method="mcquitty")
    mq.ddce <- hclust(ddce, method="mcquitty")

    plot(mq.dcos, main="cosine similarity/McQuitty")
    plot(mq.djcd, main="Jaccard index/McQuitty")
    plot(mq.dsmp, main="Simpson index/McQuitty")
    plot(wd.dtnm, main="Tanimoto index/McQuitty")
    plot(wd.ddce, main="Dice index/McQuitty")
}
par(op)
dev.off()

分類

# 実際にクラスタ数を指定して、どのIDがどのクラスタの分類されるかベクトルで
cutree(wd.dcos, k=15)

# N行1列の行列に変換してデータフレームにマージ
cbind(df, cluster = matrix(cutree(wd.dcos, k=15), nc=1))

参考
http://rstudio-pubs-static.s3.amazonaws.com/10521_be5bce1e68f44c359bc88e6b0a07ef5c.html
http://www.antecanis.com/texts/group_05/

非階層クラスタリング

k-means

• ハードクラスタリング
• $k$ 個のクラスタのいずれか1個に所属
• Rではのkmeans(データ, centers = クラスタ数, iter.max = 反復回数){stats}（デフォルトでインストールされているパッケージ）で実行
• 引数で与えるのはデータ

$$
\sum_{l=1}^k \sum_{x_i \in X_l} \parallel x_i – \mu_l \parallel^2 \rightarrow min!
$$

ただし

$k$ : 分割数
$x_i$ : 観測
$X_l$ : クラスタ $l$
$\mu_l$ : クラスタ $l$ の重心

# デフォルトでは反復回数が10と少ないので指定して実行する
USArrests.km <- kmeans(USArrests, centers = 5, iter.max = 100)

# どのIDがどのクラスタの分類されるかベクトルで
USArrests.km$cluster

# データフレームにマージ
USArrests.km <- cbind(USArrests, cluster = USArrests.km$cluster)

plot.kmeans(kmeans, data) {useful}はkmeansオブジェクトをそのままプロットできるので便利。

require(useful)
plot(USArrests.km, USArrests)

階層型クラスタリングからのk-means

初期値（クラスタの中心点）を階層型クラスタリングで算出し、それに基づいてk-meansをかける方法。

# 階層型クラスタリングからクラスタ数を指定して分類する（コサイン類似度、ウォード法）。
clusters <- cutree(hclust(dist(USArrests, method = 'cosine'), method = 'ward.D2'), k = 5)

# クラスタiの中心点を算出
clust.centroid = function(i, dat, clusters) {
  ind = (clusters == i)
  colMeans(dat[ind,])
}

# 全クラスタに適用
centers <- sapply(unique(clusters), clust.centroid, USArrests, clusters)

# k-meansの実行。sapply()の結果だと行と列が逆なので、転置して引数に与える
kmeans(USArrests, centers=t(centers)) 

参考
https://www.biostars.org/p/13143/

k-meansの初期値問題の一つの解になれば。

fuzzy c-means

• ソフトクラスタリング
• 全部で $c$ 個のクラスタのそれぞれに一定の重み $u_{li}$ ただし $i = 1, 2, .., N$ 、 $l = 1, 2, .., c$ をもって所属。チューニングパラメータ$m$が大きいとばらつきが大きくなる
• Rでは
  • cmeans {e1071}（SVMなどさまざまな機会学習系モデルのパッケージ、データは観測値のみで与える。距離行列は与えられない）
  • fanny {cluster}（クラスタリングの拡張パッケージ、データは観測でも距離行列でも指定できる）
  • FKM {fclust}（ファジィクラスタリング用のパッケージ、データは観測値のみで与える。距離行列は与えられない）

$$
\sum_{l=1}^c \sum_{i=1}^N (u_{li})^m \parallel x_i -\mu_l \parallel^2 \rightarrow min!
$$

ただし
$c$ : 分割数
$N$ : 観測の数
$u_{li}$ : 重み（所属確率）
$m$ : ファジィさを決めるパラメータ
$x_i$ : 観測
$\mu_l$ : クラスタ $l$ の重心

k-harmonic means

• ハードクラスタリング
• 調和平均を使う
• k-meansや混合分布モデルほど初期値に影響されない
• Rではパッケージがない模様

$$
\sum_{i=1}^N \frac{k}{\sum_{l=1}^k \frac{1}{\parallel x_i -\mu_l \parallel^2}} \rightarrow min!
$$

ただし
$k$ : 分割数
$N$ : 観測の数
$x_i$ : 観測
$\mu_l$ : クラスタ $l$ の重心

混合分布モデル／潜在クラスモデル

• 混合分布モデル：特徴量が連続量
• 潜在クラスモデル：特徴量が名義尺度

付けたい分類があらかじめ決まっている場合寄りの手法になる（従属変数あり、教師あり学習）

EMアルゴリズムで推定するので、EMアルゴリズムという手法名にされていることもある。
Rの{mclust}は正規分布の混合分布を前提、{flexmix}は正規分布以外も可能

http://d.hatena.ne.jp/EulerDijkstra/20130618/1371552902
http://nhkuma.blogspot.jp/2013/08/blog-post_13.html

mclustのほうが限定されているが精度は高い？

sparse dataに対するクラスリング

skmeans{skmeans}を使う

変数をクラスタリングする

これまでは観測（レコード、observation）のクラスタリングだったが、
observationではなく変数をクラスタリングするなら{ClustOfVar}パッケージが便利。

質的変数を含むデータでもクラスタリング可能で、非階層型クラスタリング、階層型クラスタリングいずれもできる。

階層型クラスタリング

hclustvar(X.quanti = data[,c(1,6:20)], X.quali = data[,2:5])

非階層型クラスタリング

kmeansvar(X.quanti = data[,c(1,6:20)], init = 3)

※hclustvar()の中のPCAmixdata::recod()にはrename.levelの指定があるので自動的に質的変数のダミー変数に変数名をつけてくれるが、kmeansvar()ではなぜかその指定がなく、質的変数を含むとエラーが発生する（バグ）。

階層型クラスタリングからの非階層型クラスタリング

tree <- hclustvar(X.quanti = data[,c(1,6:20)], init = 3)
plot(tree)
part_init <- cutreevar(tree, 5)$cluster
part <- kmeansvar(X.quanti = data[,c(1,6:20)], init=part_init, matsim=TRUE)
summary(part)
part$sim

データの加工や分析で使うRの使い方 の記事一覧

marketechlabo
 
3 Users
19 Pockets

Rにおける代表的な一般化線形モデル（GLM）の実装ライブラリまとめ
https://www.marketechlabo.com/r-glm-libraries/

marketechlabo
 
8 Users
19 Pockets

Google ColaboratoryでRを使う
https://www.marketechlabo.com/google-colaboratory-with-r/

marketechlabo
 
3 Pockets

Rのdata.tableパッケージの使える関数一覧
https://www.marketechlabo.com/r-data-table-functions/

marketechlabo
 
64 Shares
19 Users
53 Pockets

Rのおすすめパッケージ2019年版
https://www.marketechlabo.com/r-best-packages/

marketechlabo
 
15 Users
33 Pockets

Rを使ったXGBoostの高度なパラメータチューニングと細かいノウハウ
https://www.marketechlabo.com/r-xgboost-tuning/