XGBoostは機械学習手法として

• 比較的簡単に扱える
• 目的変数や損失関数の自由度が高い（欠損値を扱える）
• 高精度の予測をできることが多い
• ドキュメントが豊富（日本語の記事も多い）

ということで大変便利。

ただチューニングとアウトプットの解釈については解説が少ないので、このあたりについて説明する。

XGBoostとは？

勾配ブースティングのとある実装ライブラリ（C++で書かれた）。イメージ的にはランダムフォレストを賢くした（誤答への学習を重視する）アルゴリズム。RとPythonでライブラリがあるが、ここではRライブラリとしてのXGBoostについて説明する。

XGBoostのアルゴリズム自体の詳細な説明はこれらを参照。

• https://zaburo-ch.github.io/post/xgboost/
• https://tjo.hatenablog.com/entry/2015/05/15/190000
• グラフィカルな説明
  http://arogozhnikov.github.io/2016/06/24/gradient_boosting_explained.html

この記事では具体的なライブラリの使い方を中心に説明する。

2値分類だけでなく、連続量の回帰分析、多クラス分類、ポアソン回帰、Cox回帰（生存時間分析）などにも対応している。

データセットと前処理

House Sales in King County, USA
米国のワシントン州のキング郡の住宅価格のデータ。価格（連続量）を予測する回帰モデルを構築する。

データセットの主な留意点

• 21613行21変数
• 最初の列が識別子（id）→除外
• 2列目が20141009T000000形式の日付（date）
• 3列目が目的変数（price）
• 位置情報はzipcodeとlatとlongがあるが、zipcodeをfactorにしてlatとlongを除外
• それ以外は数値型変数なので型変換の必要なし

以上の処理をしたデータのうち80%を学習データ、20%をテストデータとして分割する。

require(data.table)
data.dt <- fread("kc_house_data.csv")
data.dt[,id:=NULL]
data.dt[,date:=as.Date(date, format='%Y%m%d')]
data.dt[,zipcode:=as.factor(zipcode)]
data.dt[,lat:=NULL]
data.dt[,long:=NULL]
nr <- nrow(data.dt)
train <- sample(nr, nr*0.8)
train.dt <- data.dt[train] # 学習データ
test.dt <- data.dt[-train] # 検証データ

手順

1. モデル構築用行列データの生成
2. パラメータチューニングしながらモデルの構築
3. 予測、評価

モデル構築用行列データの生成

XGBoostではデータをDMatrixという固有の形式で扱う。これは説明変数と目的変数が入った特殊な行列の形式で、Rの他のパッケージでは扱うことができない。DMatrixデータそのものをバイナリファイルとして保存することも可能で、Rで生成したDMatrixのバイナリをPythonで読み込むことや、その逆もできる。

まずこの形式のデータを生成する。

データフレームやdata.tableを
matrixまたはdgCMatrix形式のモデル行列に変換し、
それをxgb.DMatrix()関数でDMatrix形式にする。

学習データtrain.dtというdata.tableの正解ラベルの列がpriceで、それ以外のすべての列を説明変数とする場合

require(xgboost)
require(Matrix)
options(na.action='na.pass')
train_dmat <- xgb.DMatrix(
  sparse.model.matrix(price ~ ., data = train.dt),
  label = train.dt[, price]
)
options(na.action='na.omit')

欠損値を含むデータを扱う場合、行列の生成関数を実行する前にoptions(na.action='na.pass')を実行しておく必要がある（このデータには欠損値は含まないが、説明のため入れておいた）。

この例ではいったんMatrixパッケージのsparse.model.matrix()関数でdgCMatrix形式の行列（疎行列）を生成した。

xgb.DMatrix()関数は

xgb.DMatrix(モデル行列, label = 正解データのベクトル, weight = 行のサンプリングウェイト)

labelは

• 2値分類ではTRUEを1、FALSEを0にする
• 連続量の回帰ではそのまま
• 多項分類では、クラスのラベルを0から始まる整数にする。3クラス分類であれば{0, 1, 2}に変換する。{1, 2, 3}ではNG

weightでは学習する際に行を採用する率の重みづけを指定することができる。たとえば直近のデータをより重めに抽出する時などに指定する。このパラメータを指定しなければ均等に抽出する。形式はデータの行数と同じ長さのベクトルになる。

labelとweightは学習データの時には必要。予測用データ（正解が未知）の場合にはなくても生成できる。その場合に生成されたDMatrixは学習用の関数に投入はできず、予測用の関数にのみ引数として与えることができる。

RセッションとDMatrixデータの罠

Rのsave()やsave.image()関数ではDMatrixのデータを保存できない。
見かけ上オブジェクトがあるように見えるが、データの実体がなく、アクセスしようとするとRのセッションごと落ちてしまう。
save.image()とは別にxgb.DMatrix.save(オブジェクト名, 'ファイル名')でファイルに保存し、別のセッションで使う際にxgb.DMatrix('ファイル名')で読み込む必要がある。

気を付けておくべきなのが分散処理時。マスターからワーカーにRのセッション経由でDMatrixデータを送ることができず、ワーカーで送られたはずのDMatrixデータにアクセスを試みるとやはりRのプロセス自体が落ちる。

バイナリファイル経由で渡すか、データフレームで渡してからワーカー側でDMatrixを生成する必要がある。

DMatrix形式を扱う関数

DMatrix形式は基本的に直接走査するものではなく、その中の値を参照することもできない。
ただ以下のコマンドで一部の情報を取得することができる。

• dim(train_dmat): 行数、列数を取得
• getinfo(train_dmat, 'label'): 目的変数の値を取得

XGBoostの学習用関数とパラメータ

学習（モデルの構築）用関数

xgb.train()関数を使う。

xgb_model <- xgb.train(
  data = train_dmat,
  nrounds = 1000,
  params = l_params
)

• dataで先に指定したDMatrixを指定する。目的変数と説明変数の指定はDMatrixに含まれているため、ここでモデル式は不要。
• nroundsで繰り返し計算回数（つまり木の数）を指定
• paramsにパラメータをリストとして与える。

パラメータ

パラメータの種類

• booster: ブースターの種類。’gbtree’, ‘gblinear’, or ‘dart’から選ぶ。よくわからなくてもとりあえず'gbtree'を指定しておけばいい
• objective: 目的変数の種類
  • 回帰: 'reg:linear'（線形回帰、デフォルト）
  • 2クラス分類: 'binary:logstic'（確率を返す）, 'binary:logsticraw'（確率を返す）
  • 多クラス分類: 'multi:softmax'（所属グループを返す）, 'multi:softprob'（グループごとの所属確率を返す）
  • 順位: 'rank:pairwise'
  • ポアソン: 'count:poisson'
  • 生存: 'survival:cox'
• eval_metric: 最小化もしくは最大化する評価関数（損失関数や精度）を指定する。目的変数の種類に合ったものを選択する。以下から選択するか、独自のカスタム関数を指定することもできる（後述）。
  • 回帰: 'rmse'（デフォルト）, 'mae', 'logloss'
  • 2クラス分類: 'error'（デフォルト）, 'auc'
  • 多クラス分類: 'merror'（デフォルト）'mlogloss'
  • 順位: 'map'（デフォルト）, 'ndcg'
• eta: 各ステップの学習幅（学習率）。[0,1]の値をとる。値が小さいと学習が進みにくい（時間がかかる）一方で過学習に陥りにくい。0.01～0.2の値になることが多いらしい※。デフォルトは0.3
• max_depth: （木の複雑さ）最大の木の深さ。値が大きいと木が複雑になり過学習が発生しやすくなる。3～10の値になることが多いらしい※デフォルトで6
• gamma: （木の複雑さ）損失関数の減少がこの値を超える時にのみ分割を進める。指定する場合、評価関数によって値が異なるので気を付ける。デフォルトで0
• min_child_weight: （木の複雑さ）分割中にノードの重みがこれを超えた時点で分割をやめる。値が大きいと木がシンプルになり、過学習しにくくなる。デフォルトで1
• subsample: （サンプリング）各ステップの木を作る際に用いるレコードの数をサンプリングする割合。サンプリングすると過学習を防げる。0.5～1の値になることが多いらしい※。デフォルトで1（サンプリングしない）
• colsample_bytree: （サンプリング）各ステップの木を作る際に用いる列の数をサンプリングする割合。サンプリングすると過学習を防げる（データにfactor型を含む場合は微妙？）。0.5～1の値になることが多いらしい※。デフォルトで1（サンプリングしない）
• alpha: （正則化）L1正則化項の重み。デフォルトで0
• lambda: （正則化）L2正則化項の重み。デフォルトで1

詳細は
https://github.com/dmlc/xgboost/blob/master/doc/parameter.rst

これらを以下のようにリストにする

l_params = list(
  booster = 'gbtree',
  objective = 'reg:linear',
  eval_metric = 'mae',
  eta = 0.1,
  max_depth = 3,
  min_child_weight = 2,
  colsample_bytree = 0.8
)

繰り返し計算（ブースティング）

まずブースティングの繰り返し回数（木の数）を指定する必要がある。回数を増やすほど学習データに対するフィットはよくなっていくが、過学習になる。

具体的な最適な繰り返しの回数の決め方を紹介する。

xgb.cv()関数で学習データにおけるクロスバリデーションで決める

簡単な方法。学習データでクロスバリデーションをして評価関数の値を繰り返し計算とともにウォッチし、これ以上改善しなくなるタイミングで計算をストップする。
つまり当てはまりが最大になる点でストップするということ。

準備

• 学習データ：train.dt

# モデル構築用行列データの生成
previous_na_action <- options()$na.action
options(na.action='na.pass')
## 学習データ
train_dmat <- xgb.DMatrix(
  sparse.model.matrix(price ~ ., data = train.dt),
  label = train.dt[,price]
)
options(na.action=previous_na_action) # NAに対する扱いを元に戻しておく

# パラメータ
l_params = list(
  booster = 'gbtree',
  objective = 'reg:linear',
  eval_metric = 'mae',
  eta = 0.1,
  max_depth = 3,
  min_child_weight = 2,
  colsample_bytree = 0.8
)

モデルの構築

# クロスバリデーションの実行
xgb_cv <- xgb.cv(
  data = train_dmat, 
  nrounds = 50000, # 最大の繰り返し回数を指定。十分大きな値を指定する。
  nfold = 5, # クロスバリデーションの分割数を指定
  params = l_params,
  early_stopping_rounds = 100 # ある回数を基準としてそこから100回以内に評価関数の値が改善しなければ計算をストップ
)

出力

##### xgb.cv 5-folds
    iter train_mae_mean train_mae_std test_mae_mean test_mae_std
       1      487198.21     1035.7238     487073.90     4620.368
       2      438544.62      935.0864     438456.06     4889.937
       3      394779.90      849.8530     394612.01     4875.269
       4      355485.54      765.7785     355513.51     4897.084
       5      320385.53      708.4202     320284.82     4911.344
---                                                             
    2144       47399.47      201.3172      71690.47     2175.446
    2145       47396.24      200.7874      71691.09     2175.510
    2146       47391.42      200.6109      71692.49     2175.735
    2147       47383.61      201.4332      71690.33     2178.380
    2148       47378.26      201.1318      71694.01     2178.797
Best iteration:
 iter train_mae_mean train_mae_std test_mae_mean test_mae_std
 2048       47974.79      214.7405      71682.65     2194.454

xgb_cv$best_iterationがベストの木の数となる。これをnroundsに指定してモデルを構築

xgb_model <- xgb.train(
  data = train_dmat,
  nrounds = xgb_cv$best_iteration,
  params = l_params
)

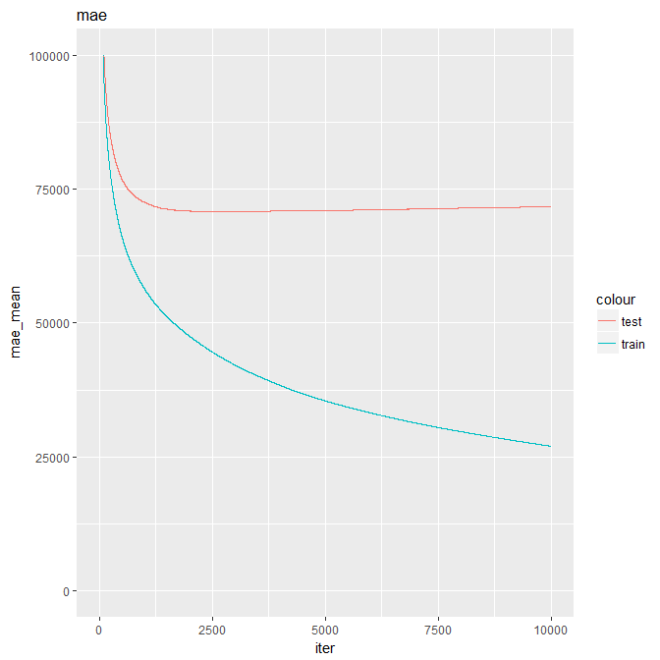
iterationの回数とmaeの推移は以下のようになるが、検証用データ（赤）のmaeがn=2000+ちょっとのあたりで極小になっているのがわかる。
この極小になるiterを検出してそれ以降のiterをやめるのを自動で行う。

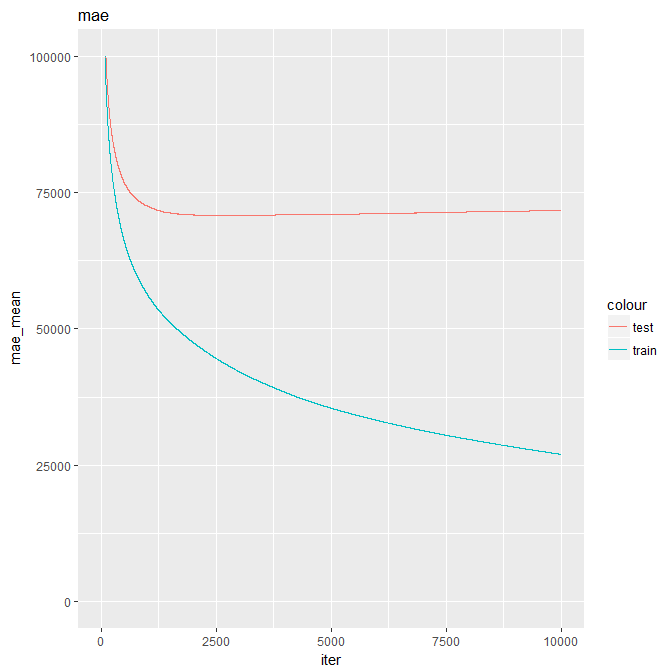
xgb_cv$evaluation_log %>% 
  ggplot(aes(x=iter)) + 
  geom_line(aes(y=train_mae_mean, col='train')) + 
  geom_line(aes(y=test_mae_mean, col='test')) + 
  ggtitle("mae") + ylab("mae_mean") + ylim(0,100000)

watchlistを指定して検証データに対する評価関数の値を見て決める

検証用データを用意し、検証用データに対する予測精度を計算の繰り返しとともにモニタリングし、予測精度が極大になる回数でストップする。

1. 最大指定した繰り返し計算回数の中で
2. 検証データにおける評価関数の値を監視し、
3. これ以上改善しなくなるタイミングで計算をストップする。

準備

• 学習データ：train.dt
• 検証データ：test.dt

# モデル構築用行列データの生成
previous_na_action <- options()$na.action
options(na.action='na.pass')
## 学習データ
train_dmat <- xgb.DMatrix(
  sparse.model.matrix(price ~ ., data = train.dt),
  label = train.dt[,price]
)
## 検証データ
test_dmat <- xgb.DMatrix(
  sparse.model.matrix(price ~ ., data = test.dt),
  label = test.dt[,price]
)
options(na.action=previous_na_action) # NAに対する扱いを元に戻しておく

# パラメータ
l_params = list(
  booster = 'gbtree',
  objective = 'reg:linear',
  eval_metric = 'mae',
  eta = 0.1,
  max_depth = 3,
  min_child_weight = 2,
  colsample_bytree = 0.8
)

モデルの構築

xgb_model <- xgb.train(
  data = train_dmat,
  nrounds = 50000, # 最大の繰り返し回数を指定。十分大きな値を指定する。→1
  verbose = 2, # 繰り返し過程を表示する
  params = l_params,
  watchlist = list(train = train_dmat, eval = test_dmat), # このデータに対する評価関数の値をモニタリングする→2
  early_stopping_rounds = 100 # ある回数を基準としてそこから100回以内に評価関数の値が改善しなければ計算をストップ→3
)

これで評価関数の値が最適になる木の数でのモデルが生成される。

2クラス分類での例（データ）

train_dmat <- xgb.DMatrix(
  sparse.model.matrix(default.payment.next.month ~ ., data = train.dt),
  label = train.dt[,default.payment.next.month]
)
test_dmat <- xgb.DMatrix(
  sparse.model.matrix(default.payment.next.month ~ ., data = test.dt),
  label = test.dt[,default.payment.next.month]
)
xgb_model <- xgb.train(
  data = train_dmat,
  nrounds = 10000,
  max_depth = 2,
  params = list(booster = 'gbtree', ojective = "binary:logistic", eval_metric = 'auc'),
  watchlist = list(train = train_dmat, eval = test_dmat),
  early_stopping_rounds = 100
)
xgb_pred <- predict(xgb_model, test_dmat)

チューニング

パラメータをグリッドサーチによってチューニングする。

パラメータチューニングの指針

チューニング対象のパラメータ

• eta: 学習率、デフォルトで0.3
• max_depth: 最大の木の深さ、デフォルトで6
• min_child_weight: 、デフォルトで1
• （gamma: 、デフォルトで0）
• subsample: 行数のサンプリング率、デフォルトで1
• colsample_bytree: 特徴量（列）の数のサンプリング率、デフォルトで1
• （alpha: L1正則化項の重み、デフォルトで0）
• （lambda: L2正則化項の重み、デフォルトで1）
• nrounds: 繰り返し計算回数、必ず指定

（）はやらなくてもいい

手順

1. 学習率etaの初期値を決める。
   XGBoostでは基本的に学習率etaが小さければ小さいほどいい。
   ただし小さくすると学習に時間がかかるので、何度も学習を繰り返すグリッドサーチでは他のパラメータをチューニングするためにある程度小さいetaの値を決めておいて、そこで他のパラメータをチューニングする。
   他のパラメータの値が決まってからetaを時間との兼ね合いでチューニングする（小さくしていく）。
   デフォルトの0.3では大きいので0.01～0.1あたりに設定する。
2. 木の複雑さを指定するパラメータmax_depth, min_child_weightを同時に決める
3. （gammaを決める）
4. データのサンプリングの度合いを指定するパラメータsubsample, colsample_bytreeを同時に決める。いずれも0.5から1の間あたりで設定するといい。
5. （正則化パラメータalpha, lambdaを同時に決める）
6. ブースティングの繰り返し回数nroundsはグリッドサーチではなく、上記のパラメータの組合せごとに繰り返し計算（ブースティング）の手順で決める。
7. etaを小さくしていく

参考

• https://blog.cambridgespark.com/hyperparameter-tuning-in-xgboost-4ff9100a3b2f
• https://www.analyticsvidhya.com/blog/2016/03/complete-guide-parameter-tuning-xgboost-with-codes-python/

caretの落とし穴

Rの機械学習におけるグリッドサーチはcaretパッケージを使うことが多い。
XGBoostではデータフレームを最終的にDMatrix形式に変換するわけだが、caretではデータフレームを通常のmatrix形式経由でDMatrixに変換する。巨大な行列でメモリ節約をするdgCMatrix形式でないため、モデル行列が大きくなるとメモリ不足エラーを引き起こす。
データフレームの説明変数の列数が多くなくても、ラベルの数が膨大になるfactor型変数を扱うとアウト

そこでグリッドサーチは自前で実装できるようにしておいたほうがいい。
そうしておけばグリッドサーチのパターンごとの学習済みモデルをバイナリ保存することもできるし、パターンごとの学習結果やエラー関数の詳細をテキストファイルに出力することもできる。繰り返し計算の回数やモデル構築にかかる時間なども出力できるので、さまざまな観点からのパラメータ選択が柔軟にできる（精度はそこそこに構築にかかる時間が短いパラメータの採択など）。

自前で実装するときのポイント

グリッドサーチをする時はパターンごとにをコアを分ける分散処理を想定してしまうが、マシン1台で学習する場合は複数コアであったとしてもシリアルで十分。というよりシリアルが望ましい。
そもそもXGBoost自体がマルチコア対応しているため、こちらから実行するコマンドがシリアルであったとしても効率的に分散処理をしてくれる。逆にdoParallelで明示的に分散処理をするとxgb.train()側が行う分散処理とコンフリクトし、かえって無駄に時間がかかってしまう。

自前のグリッドサーチ実装例

1. パラメータの組み合わせを格納したデータフレームを用意しておいて
2. 行ループしながら
3. 各行のパラメータを読み込んでxgb.train()に代入
4. 結果を保存
   1. 各行で生成したモデルオブジェクトをバイナリファイルとして保存
   2. 各行における評価関数の値の推移をCSVファイルとして保存
   3. パラメータのデータフレームに評価関数の値の最大値／最小値を付加したデータフレームを返す

これを

1. max_depth, min_child_weight
2. subsample, colsample_bytree

についてそれぞれ行う。

自前実装だと検証用に様々なファイルを保存しておくことができる。

準備

まず学習用の関数と各種データを保存するファイル名を定義する。

# ライブラリ
require(xgboost)
require(Matrix)
require(dplyr)
require(doParallel)
registerDoParallel(detectCores()-1)

mae <- function(x) sum(abs(x))/length(x)

# パラメータの組み合わせを定義したデータフレームと行番号を引数とする関数
gridXgb <- function(records, i){

  # パラメータの組み合わせを定義したデータフレームから行の取り出し
  record <- records[i,]

  # モデル構築用行列データの生成
  previous_na_action <- options()$na.action
  options(na.action='na.pass')
  ## 学習データ
  train_dmat <- xgb.DMatrix(
    sparse.model.matrix(price ~ ., data = train.dt),
    label = train.dt[,price]
  )
  ## 検証データ
  test_dmat <- xgb.DMatrix(
    sparse.model.matrix(price ~ ., data = test.dt),
    label = test.dt[,price]
  )
  options(na.action=previous_na_action) # NAに対する扱いを元に戻しておく

  # パラメータのリスト
  l_params <- list(
    booster           = 'gbtree',
    objective         = 'reg:linear',
    eval_metric       = 'mae',
    eta               = record$eta,
    gamma             = 0,
    max_depth         = record$max_depth,
    min_child_weight  = record$min_child_weight,
    subsample         = record$subsample,
    colsample_bytree  = record$colsample_bytree
  )

  # モデルの構築
  elapsed <- system.time({
    xgb_model <- xgb.train(
      data = train_dmat,
      nrounds = 50000, # 最大の繰り返し回数を指定。十分大きな値を指定する。
      verbose = 2,
      params = l_params,
      watchlist = list(train = train_dmat, eval = test_dmat),
      early_stopping_rounds = 100 # ある回数を基準としてそこから100回以内に評価関数の値が改善しなければ計算をストップ
    )
  })[3]

  # モデルオブジェクトをバイナリファイル保存
  xgb.save(xgb_model, paste0(MODEL_FILE, i, '.xgb'))

  # 検証データにおける予測値と正解の対応表をCSVファイルに保存
  predicted <- cbind(
    i = i,
    label = test.dt[,price],
    predicted = predict(xgb_model, newdata=test_dmat)
  ) %>% as.data.table
  predicted %>% fwrite(paste0(PREDICT_FILE, i, '.csv'))

  # 評価関数の値をCSVファイルに追記
  predicted[, .(eval_mae=mae(label-predicted), N=.N, elapsed=elapsed), by = i] %>% fwrite(OPTIMUM_EVAL_FILE, append=T)

  # 学習（最適化）の過程をCSVファイルに追記
  cbind(i=i, xgb_model$evaluation_log) %>% fwrite(EVAL_LOG_FILE, append=T)
}

max_depth, min_child_weightを決める

グリッドサーチを行う。まず第1ステップとして学習率を0.1に固定し、max_depthとmin_child_weightをグリッドサーチする。
colsample_bytreeとsubsampleは1（デフォルトの値）にする。

# ステップ1
# 保存するファイル名のベースを定義
MODEL_FILE        = 'xgb_model_step1_' # xgb_model_step1_1.xgb, xgb_model_step1_2.xgb, ... という名前のファイルとして出力
PREDICT_FILE      = 'xgb_pred_step1_'  # xgb_pred_step1_1.csv, xgb_pred_step1_2.csv, ... という名前のファイルとして出力
OPTIMUM_EVAL_FILE = 'xgb_mae_step1.csv'
EVAL_LOG_FILE     = 'xgb_log_step1.csv'

# パラメータの組み合わせを定義したデータフレーム
tune_params = expand.grid(
  eta = 0.1,
  max_depth = c(2,4,6,8,10),
  min_child_weight = c(1,1.5,2,2.5,3),
  colsample_bytree = 1,
  subsample = 1
) %>% as.data.table
tune_params[,i:=.I]

# パラメータの組み合わせをCSVファイルに保存しておく
tune_params %>% fwrite('tune_params_step1.csv')

# ループ処理
# foreach()は使うが、%do%でシリアル扱いにしておく
foreach(
  i = 1:nrow(tune_params),
  .verbose = T, .multicombine = T, .packages='data.table' # .combine=listはおかしなことになる
) %do% gridXgb(tune_params, i)

出力
パラメータの組み合わせを定義したデータフレームのCSVファイル（tune_params_step1.csv）

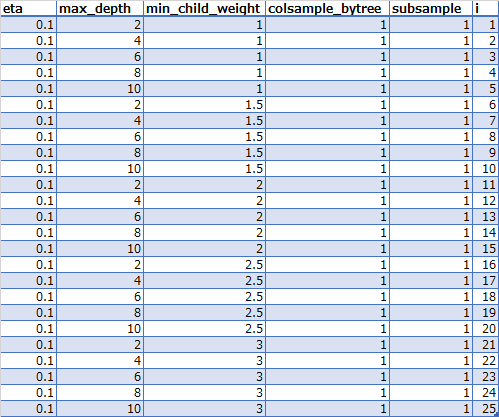
PREDICT_FILE（xgb_pred_step1_1.csv）

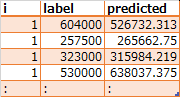
iがパラメータの組み合わせを定義したデータフレームの行番号を表す。

OPTIMUM_EVAL_FILE（xgb_mae_step1.csv）

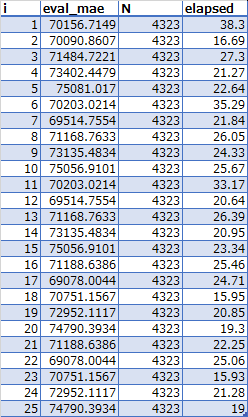
Nが予測件数、elapsedが学習にかかった時間を表す。
この結果i = 17が最適値、つまり

• max_depth = 4
• min_child_weight = 2.5

が最適値ということになる。

EVAL_LOG_FILE（xgb_log_step1.csv）

subsample, colsample_bytreeを決める

次にetaとステップ1で導いたmax_depthとmin_child_weightを固定し、max_depthとmin_child_weightをグリッドサーチする。

# 保存するファイル名のベースを定義
MODEL_FILE        = 'xgb_model_step2_' # xgb_model_step2_1.xgb, xgb_model_step2_2.xgb, ... という名前のファイルとして出力
PREDICT_FILE      = 'xgb_pred_step2_'  # xgb_pred_step2_1.csv, xgb_pred_step2_2.csv, ... という名前のファイルとして出力
OPTIMUM_EVAL_FILE = 'xgb_mae_step2.csv'
EVAL_LOG_FILE     = 'xgb_log_step2.csv'

# ステップ2
tune_params = expand.grid(
  eta = 0.1,
  max_depth = 4,
  min_child_weight = 2.5,
  colsample_bytree = c(0.5,0.6,0.7,0.8,0.9,1),
  subsample = c(0.5,0.6,0.7,0.8,0.9,1)
) %>% as.data.table
tune_params[,i:=.I]

# パラメータの組み合わせをCSVファイルに保存しておく
tune_params %>% fwrite('tune_params_step2.csv')

# ループ処理
# foreach()は使うが、%do%でシリアル扱いにしておく
foreach(
  i = 1:nrow(tune_params),
  .verbose = T, .multicombine = T, .packages='data.table' # .combine=listはおかしなことになる
) %do% gridXgb(tune_params, i)

結果

OPTIMUM_EVAL_FILE（xgb_mae_step2.csv）

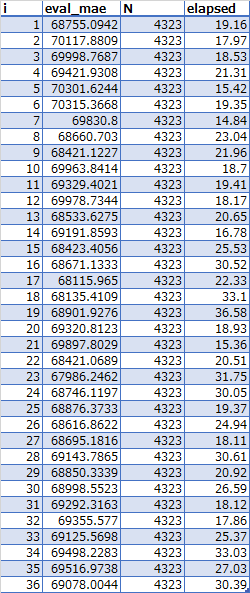
この結果i = 23が最適値。

パラメータの組み合わせ（tune_params_step2.csv）

eta	max_depth	min_child_weight	colsample_bytree	subsample	i
0.1	4	2.5	0.9	0.8	23

によると

• colsample_bytree == 0.9
• subsample == 0.8

が最適値ということになる。
（サンプリングなので改めて実行すると結果が変わることがはある。その場合どちらも精度に変わりないとみなしていい）

etaを小さくしていく

上記のパラメータの値を固定してetaを小さくしていく

# ステップ3
# 保存するファイル名のベースを定義
MODEL_FILE        = 'xgb_model_step3_' # xgb_model_step3_1.xgb, xgb_model_step3_2.xgb, ... という名前のファイルとして出力
PREDICT_FILE      = 'xgb_pred_step3_'  # xgb_pred_step3_1.csv, xgb_pred_step3_2.csv, ... という名前のファイルとして出力
OPTIMUM_EVAL_FILE = 'xgb_mae_step3.csv'
EVAL_LOG_FILE     = 'xgb_log_step3.csv'

# パラメータの組み合わせを定義したデータフレーム
tune_params = expand.grid(
  eta = c(0.01, 0.05, 0.1, 0.2, 0.3),
  max_depth = 4,
  min_child_weight = 2.5,
  colsample_bytree = 0.9,
  subsample = 0.8
) %>% as.data.table
tune_params[,i:=.I]

# パラメータの組み合わせをCSVファイルに保存しておく
tune_params %>% fwrite('tune_params_step3.csv')

# ループ処理
# foreach()は使うが、%do%でシリアル扱いにしておく
foreach(
  i = 1:nrow(tune_params),
  .verbose = T, .multicombine = T, .packages='data.table' # .combine=listはおかしなことになる
) %do% gridXgb(tune_params, i)

結果

OPTIMUM_EVAL_FILE（xgb_mae_step3.csv）

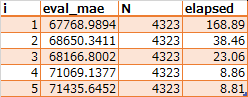
パラメータの組み合わせ（tune_params_step3.csv）

etaが0.1以下では精度がほぼ横ばいなので実行時間の短いetaを採用する。
そのほか、精度がわずかに向上する場合でも時間が極端にかかるようになったら時間の短いほうを採用することが普通である。
このように時間との兼ね合いでetaを決める。

最終的なパラメータの組み合わせは

• eta = 0.1
• max_depth = 4
• min_child_weight = 2.5
• colsample_bytree = 0.9
• subsample = 0.8

ということになる。

データの加工や分析で使うRの使い方 の記事一覧

marketechlabo
 
3 Users
19 Pockets

Rにおける代表的な一般化線形モデル（GLM）の実装ライブラリまとめ
https://www.marketechlabo.com/r-glm-libraries/

marketechlabo
 
8 Users
19 Pockets

Google ColaboratoryでRを使う
https://www.marketechlabo.com/google-colaboratory-with-r/

marketechlabo
 
3 Pockets

Rのdata.tableパッケージの使える関数一覧
https://www.marketechlabo.com/r-data-table-functions/

marketechlabo
 
64 Shares
19 Users
53 Pockets

Rのおすすめパッケージ2019年版
https://www.marketechlabo.com/r-best-packages/

marketechlabo
 
2 Users
6 Pockets

Rで時系列分析の簡単なまとめ
https://www.marketechlabo.com/r-time-series-analysis/