目次
準備
決定木(decision tree)分析をする際、まず目的変数の種類とアルゴリズムを決定する。
アルゴリズム
- CART
- CHAID
- ID3 / C4.5 / C5.0
目的変数の型
目的変数の型によって扱いが変わる
- 質的変数(2値変数):分類木→目的変数が0/1, T/Fの場合は
as.factor()でfactor型にデータ変換しておく - 量的変数:回帰木
- survivalオブジェクト
- (生起を表す2カラム)
CARTはすべて対応、C4.5/C5.0は質的変数のみ
ここではCARTアルゴリズムでツリーモデルを生成するrpartと、ランダムフォレストrangerを中心に説明する。
データセットと前処理
Default of Credit Card Clients Dataset
データセットの主な留意点
- 30000行25変数
- 最初の列が識別子(
ID)→除外 - 3列目
SEX, 4列目EDUCATION, 5列目MARRIAGEがカテゴリ変数→factorに変換 - 最終列
default.payment.next.monthが目的変数で0/1の値をとる。 - それ以外は数値型変数なので型変換の必要なし
以上の処理をしたデータのうち80%を学習データ、20%をテストデータとして分割する。
require(data.table)
data.dt <- fread("UCI_Credit_Card.csv")
data.dt[,ID:=NULL]
data.dt[,SEX:=as.factor(SEX)]
data.dt[,EDUCATION:=as.factor(EDUCATION)]
data.dt[,MARRIAGE:=as.factor(MARRIAGE)]
nr <- nrow(data.dt)
train <- sample(nr, nr*0.8)
train.dt <- data.dt[train] # 学習データ
test.dt <- data.dt[-train] # 検証データ
1回限りの決定木
実行
require(rpart)
train.dt %>%
mutate(
default.payment.next.month = as.factor(default.payment.next.month == 1)
) %>%
rpart(
formula = default.payment.next.month ~ .,
data = .,
method = 'class',
parms = list(split='information'),
control = rpart.control(minsplit = 10, cp= .001)
) -> rpart_model
- 投入するデータテーブルの変数を絞っておくと変数指定が楽
- プロットしたときのラベルをわかりやすく変換しておくといい
- 分類木の場合は目的変数をfactor型に変換しておく
- 重要なパラメータ
method(通常は目的変数の型によって自動で最適なものが選択される)- ‘class’で分類木(目的変数がfactor型)
- ‘poisson’で生起(目的変数が2カラムの生起データ)
- ‘exp’で生存(目的変数がsurvicalオブジェクト)
- ‘anova’で回帰木(目的変数が上記のいずれでもない)
parms:method = 'class'の場合、以下の指標に基づいて分割。method = 'anova'の場合は指定しないparms = list(split='gini')でジニ係数を使う(デフォルト)parms = list(split='information')でエントロピーを使う
rpart.controlminsplitは1ノードのサイズの下限cpは小さいほど細かく分岐する。あとで粗くできるので最初は細かく分けておくといい
見る
summary(rpart_model)
出力
Call:
rpart(formula = default.payment.next.month ~ ., data = ., method = "class",
parms = list(split = "information"), control = rpart.control(minsplit = 10,
cp = 0.001))
n= 24000
CP nsplit rel error xerror xstd
1 0.184880240 0 1.0000000 1.0000000 0.01206064
2 0.002245509 1 0.8151198 0.8151198 0.01117344
3 0.002151946 4 0.8074476 0.8197979 0.01119832
4 0.001060379 7 0.8003368 0.8197979 0.01119832
5 0.001000000 10 0.7971557 0.8203593 0.01120130
Variable importance
PAY_0 PAY_2 PAY_5 PAY_4 PAY_3 PAY_6 PAY_AMT3
66 18 4 3 3 3 1
Node number 1: 24000 observations, complexity param=0.1848802
predicted class=FALSE expected loss=0.2226667 P(node) =1
class counts: 18656 5344
probabilities: 0.777 0.223
left son=2 (21510 obs) right son=3 (2490 obs)
Primary splits:
PAY_0 < 1.5 to the left, improve=1478.1780, (0 missing)
PAY_2 < 1.5 to the left, improve=1168.7680, (0 missing)
PAY_3 < 1.5 to the left, improve= 869.5735, (0 missing)
PAY_4 < 0.5 to the left, improve= 758.7756, (0 missing)
PAY_5 < 1 to the left, improve= 689.8890, (0 missing)
Surrogate splits:
PAY_4 < 2.5 to the left, agree=0.900, adj=0.037, (0 split)
PAY_5 < 2.5 to the left, agree=0.900, adj=0.035, (0 split)
PAY_3 < 2.5 to the left, agree=0.899, adj=0.029, (0 split)
PAY_6 < 2.5 to the left, agree=0.899, adj=0.028, (0 split)
PAY_2 < 3.5 to the left, agree=0.898, adj=0.018, (0 split)
:
変数の重要度を確認
rpart_model$variable.importance
出力
PAY_0 PAY_2 PAY_5 PAY_4 PAY_3
1478.1783401 395.1016287 80.8746934 75.6083311 70.7895234
PAY_6 PAY_AMT3 BILL_AMT1 PAY_AMT4 BILL_AMT2
62.3976688 11.4724819 11.0370003 10.9009460 9.7894688
PAY_AMT5 EDUCATION BILL_AMT3 BILL_AMT5 BILL_AMT4
8.6928210 7.0296988 5.4445876 5.1257181 4.7143508
BILL_AMT6 PAY_AMT6 AGE PAY_AMT1
4.5410328 3.5949029 0.5542719 0.2771359
チューニング(cpを調整)
cpはツリーモデルの複雑さを表すパラメータ。値が小さいものほどモデルが細かくなる。
cpを見る
printcp(rpart_model)
plotcp(rpart_model)
出力
Classification tree:
rpart(formula = default.payment.next.month ~ ., data = ., method = "class",
parms = list(split = "information"), control = rpart.control(minsplit = 10,
cp = 0.001))
Variables actually used in tree construction:
[1] BILL_AMT1 EDUCATION PAY_0 PAY_2 PAY_3 PAY_5 PAY_6
[8] PAY_AMT3 PAY_AMT4 PAY_AMT5
Root node error: 5344/24000 = 0.22267
n= 24000
CP nsplit rel error xerror xstd
1 0.1848802 0 1.00000 1.00000 0.012061
2 0.0022455 1 0.81512 0.81512 0.011173
3 0.0021519 4 0.80745 0.81980 0.011198
4 0.0010604 7 0.80034 0.81980 0.011198
5 0.0010000 10 0.79716 0.82036 0.011201
cpを調整(cpの小さいツリーモデルからcpの大きいツリーモデルへ)
rpart_model_new <- prune(rpart_model, cp=0.0022)
プロット(2通りのライブラリで)
ビルトインのplot
par(xpd = TRUE)
plot(rpart_model_new, compress = TRUE)
text(rpart_model_new, use.n = TRUE)
(決定木のプロット例)
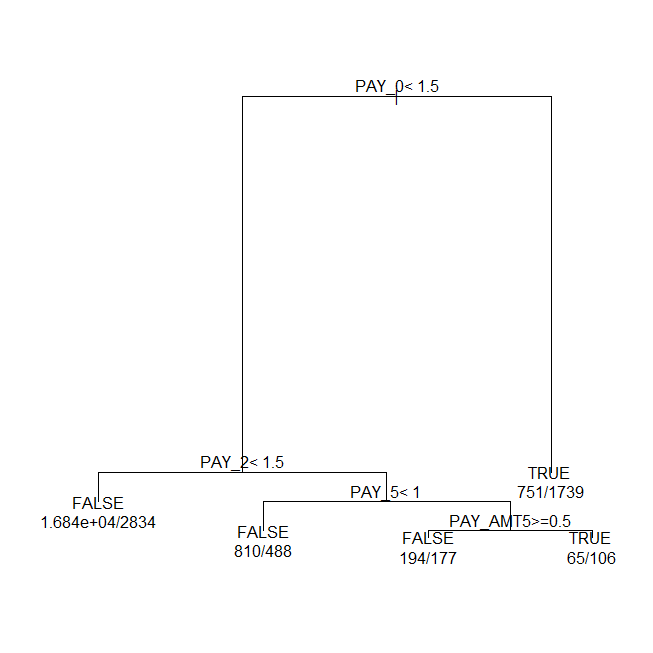
ライブラリ{rpart.plot}
require(rpart.plot)
rpart.plot(rpart_model_new)
(決定木のプロット例)
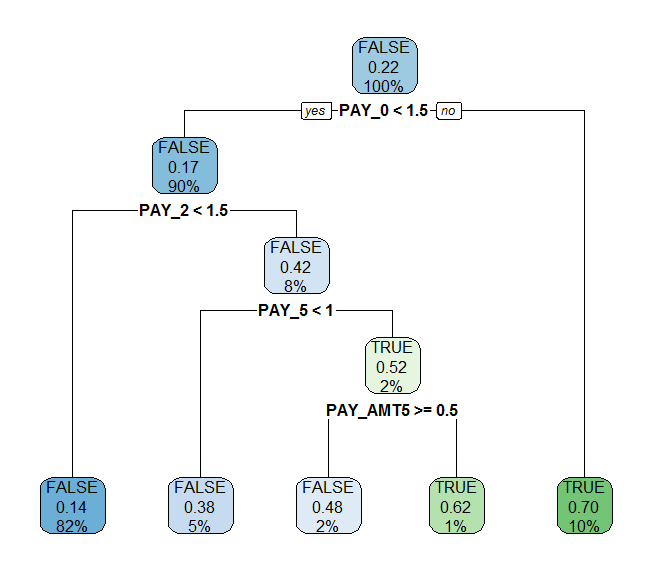
ライブラリ{partykit}
require(partykit)
plot(as.party(rpart_model_new))
plot(as.party(rpart_model_new), gp = gpar(fontsize = 9))
(決定木のプロット例)
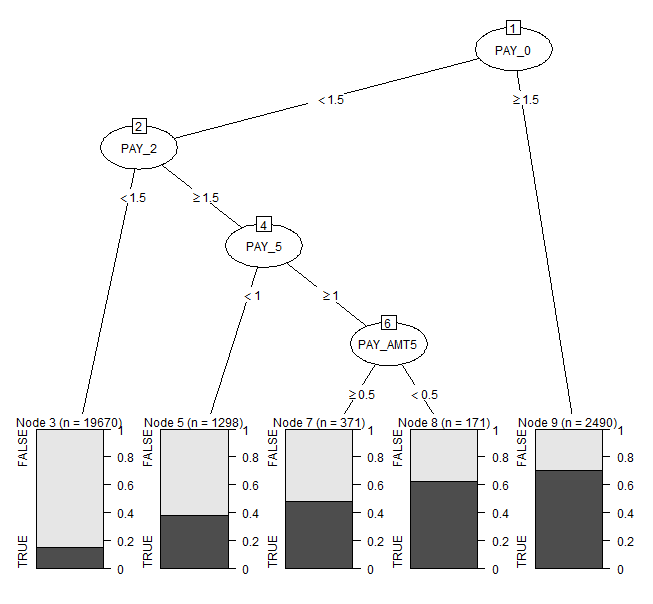
どれを使ってもいいが、使いやすいものを確保しておくといい。
分類されたノードを元データに紐づける
train.dt[, node := rpart_model_new$where]
予測
各クラスに所属する確率を予測する
predict(rpart_model_new, test.dt)
ランダムフォレスト(random forest)
rangerパッケージが便利。
以下の目的変数ごとのツリーモデルをサポートしている。
- 質的変数(2値変数):分類木→目的変数が0/1, T/Fの場合は
as.factor()でfactor型に変換しておく - 量的変数:回帰木
- survivalオブジェクト
実行(モデルの構築)
require(ranger)
require(ROCR)
# モデルの構築
ranger_model <- ranger(
formula = as.factor(default.payment.next.month) ~ ., # default.payment.next.monthが目的変数になる
data = train.dt,
num.trees = 1000,
mtry = 5,
write.forest = TRUE,
importance = 'impurity',
probability = TRUE
)
パラメータ
ランダムフォレストのハイパーパラメータは
num.trees: 試す決定木の数mtry: モデルに採用する変数の数
mtryをグリッドサーチするならcaretでmethod='ranger'を指定する(後述)。
その他の主なパラメータ
min.node.sizeでノードサイズの下限を指定できるimportanceを与えると変数の重要度を返す。回帰木と分類木では’impurity’を(ジニ係数)、生存では’permutation’を指定する(デフォルトでは重要度を返さない)。- 目的変数が質的変数の時、
probability = TRUEで確率を返す。デフォルトのFALSEではT/Fの応答(ただしfactor)を返す。確率は2列の行列で、logical型の目的変数をfactor型にしてranger()をかけている場合、2列目がTRUEとなる(FALSE,TRUEの順)
なおデフォルトでは
- 分類木ではGini係数に基づいて、
- 回帰木では分散に基づいて、
- 生存モデルではログランクに基づいて
分割する。
戻り値
戻り値のrangerオブジェクトはリストで、よく使う属性が
predictionsが予測結果variable.importanceが変数の重要度
なお結果のprediction.errorは
- 分類木では誤分類の割合
- 回帰木では平均二乗誤差(MSE)
- 生存モデルではc-index
が使われる。
予測
predict()関数を使う。新しいデータセットを指定する引数の名前がdata(newdataではない!)
ranger_pred <- predict(ranger_model, data=test.dt)
実行結果が予測結果値そのものではなく、予測結果値を含むリスト。予測結果値は
ranger_pred$predictions
で取り出す。
2値分類時は形式が特殊になる。
ranger()の実行時にprobability = TRUEを指定している場合は1列目がFALSEの確率、2列目がTRUEの確率となる行列
→TRUEとなる確率を取り出すには
ranger_pred <- predict(ranger_model, data=test.dt)$predictions[,2]
probability = FALSEを指定している場合はTRUE/FALSEの結果になる
ranger_pred <- predict(ranger_model, data=test.dt)$predictions
モデルの評価
partial dependence plot
partial dependence plot(部分従属プロット)を描くにはedarfパッケージを使う。ranger以外にもrandomForest, RandomForest, rfsrcのランダムフォレストオブジェクトに対応している。
require(edarf)
pd <- partial_dependence(ranger_model, vars = c('default.payment.next.month', 'BILL_AMT1'), data = as.data.frame(train.dt))
plot_pd(pd)
partial_dependence()の引数dataはdata.tableではダメで、data.frameでなければならない
このパッケージedarfはランダムフォレストの診断に便利。
https://qiita.com/nakamichi/items/bed7a2f180ea9ce86d94
精度
{ROCR}パッケージでAUCやROC曲線をプロットできる
ranger_predが結果(レスポンス)の場合、confusion matrix(混同行列)
# 予測結果のレスポンスのベクトルを取り出す
ranger_pred <- predict(ranger_model, data=test.dt)$predictions
# confusion matrix
table(ranger_pred, test.dt[,default.payment.next.month])
ranger_predが確率の場合、AUCを計算する
# 予測結果の確率のベクトルを取り出す
ranger_pred <- predict(ranger_model, data=test.dt)$predictions[,2]
# ROCオブジェクトを生成
rocr_pred <- prediction(ranger_pred, test.dt[,default.payment.next.month])
# ROCオブジェクトからAUCを取り出す
performance(rocr_pred, 'auc')@y.values
ROC曲線
performance(rocr_pred, "tpr", "fpr") %>% plot
{caret}のtrain()ハイパーパラメータをグリッドサーチ
train.dt %>%
mutate(default.payment.next.month = as.factor(default.payment.next.month)) %>% # 目的変数はfactor型
mutate_if(is.factor, funs(make.names)) %>% # factor型のラベルが整数値になっているとNGなので変換
train(
default.payment.next.month ~ .,
data = .,
method = 'ranger',
metric = 'ROC',
num.trees = 1000,
na.action = na.omit,
tuneGrid = expand.grid(mtry = 3:10, splitrule = 'gini', min.node.size = 1), # グリッドサーチしないパラメータも指定が必要
trControl = trainControl(method = 'cv', number = 5, allowParallel = TRUE, classProbs = TRUE, summaryFunction = twoClassSummary)
) -> ranger_train
na.actionはレコードにNAを含む場合の扱いを指定する。デフォルトはna.failで処理に失敗する。NAを含む行を除外して実行する場合はna.omitを指定する。- 分類木では(ロジスティック回帰のようなその他のクラス分類においても)
metricに’Accuracy’, ‘Kappa’, ‘ROC’を指定できる。ROCを使う場合、trControlの引数にclassProbs = TRUEを加える必要がある。
出力
Random Forest
24000 samples
23 predictor
2 classes: 'X0', 'X1'
No pre-processing
Resampling: Cross-Validated (5 fold)
Summary of sample sizes: 19200, 19200, 19201, 19200, 19199
Resampling results across tuning parameters:
mtry ROC Sens Spec
3 0.7741246 0.9494532 0.3628346
4 0.7715815 0.9468802 0.3706940
5 0.7701622 0.9447362 0.3721916
6 0.7685357 0.9433962 0.3721927
7 0.7683098 0.9434497 0.3729410
8 0.7672948 0.9430209 0.3749983
9 0.7674797 0.9420025 0.3757476
10 0.7664394 0.9422705 0.3755605
Tuning parameter 'splitrule' was held constant at a value of gini
Tuning parameter 'min.node.size' was held constant at a value of 1
ROC was used to select the optimal model using the largest value.
The final values used for the model were mtry = 3, splitrule = gini
and min.node.size = 1.
参考 – rpartに対してtrainすると
train.dt %>%
mutate(
default.payment.next.month = as.factor(make.names(default.payment.next.month == 1)) # 目的変数はfactor型で、factor型のラベルが「TRUE」「FALSE」になっているとNGなので変換
) %>%
train(
default.payment.next.month ~ .,
data = .,
na.action = na.omit, # or na.fail
method = 'rpart',
parms = list(split='information'),
control = rpart.control(minsplit = 10, cp = 0.001),
metric = 'ROC',
trControl = trainControl(method = 'repeatedcv', number = 10, repeats = 10, allowParallel = TRUE, classProbs = TRUE, summaryFunction = twoClassSummary),
) -> rpart_train
出力
CART
24000 samples
24 predictor
2 classes: 'FALSE.', 'TRUE.'
No pre-processing
Resampling: Cross-Validated (10 fold, repeated 10 times)
Summary of sample sizes: 21600, 21600, 21600, 21600, 21599, 21600, ...
Resampling results across tuning parameters:
cp ROC Sens Spec
0.002151946 0.6927440 0.9580994 0.3380787
0.003181138 0.6926181 0.9564967 0.3432241
0.189371257 0.5000000 1.0000000 0.0000000
ROC was used to select the optimal model using the largest value.
The final value used for the model was cp = 0.002151946.
cpの値を探索することになる。
データの加工や分析で使うRの使い方 の記事一覧